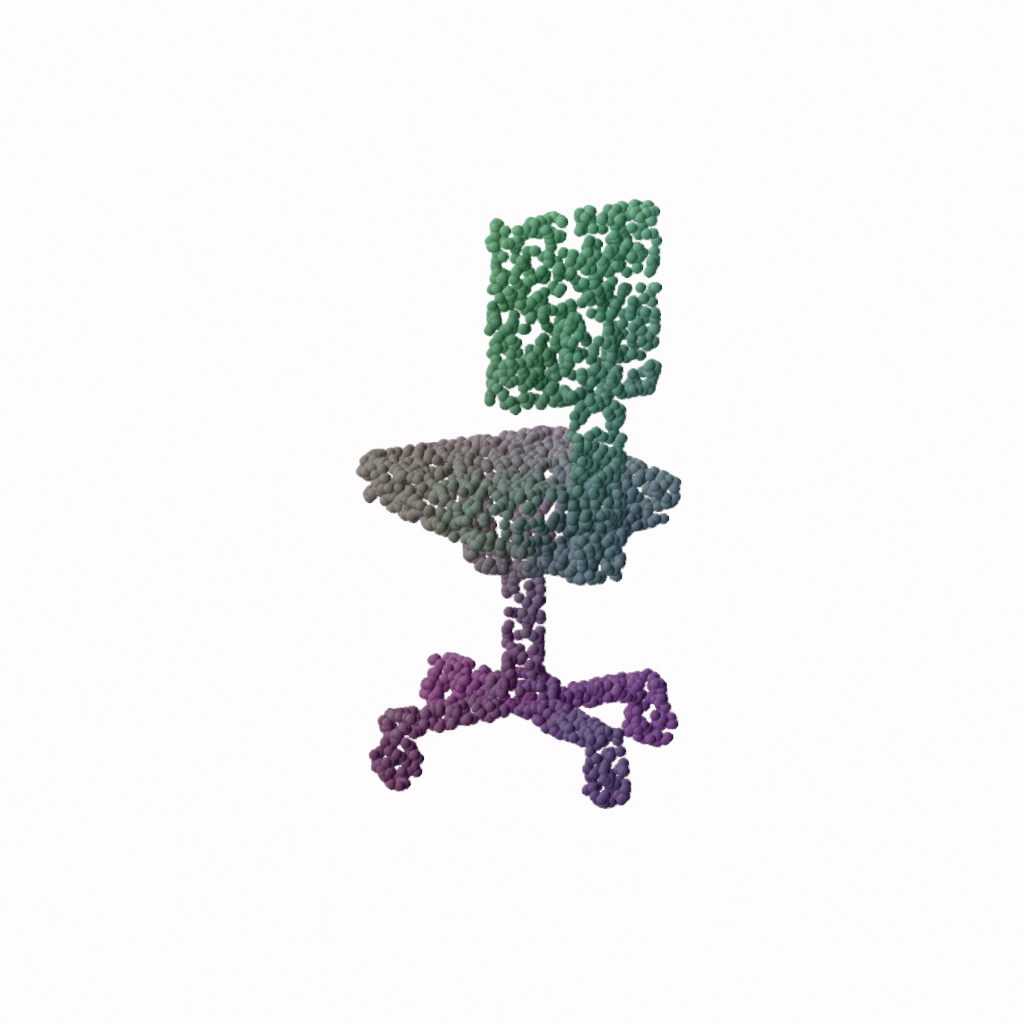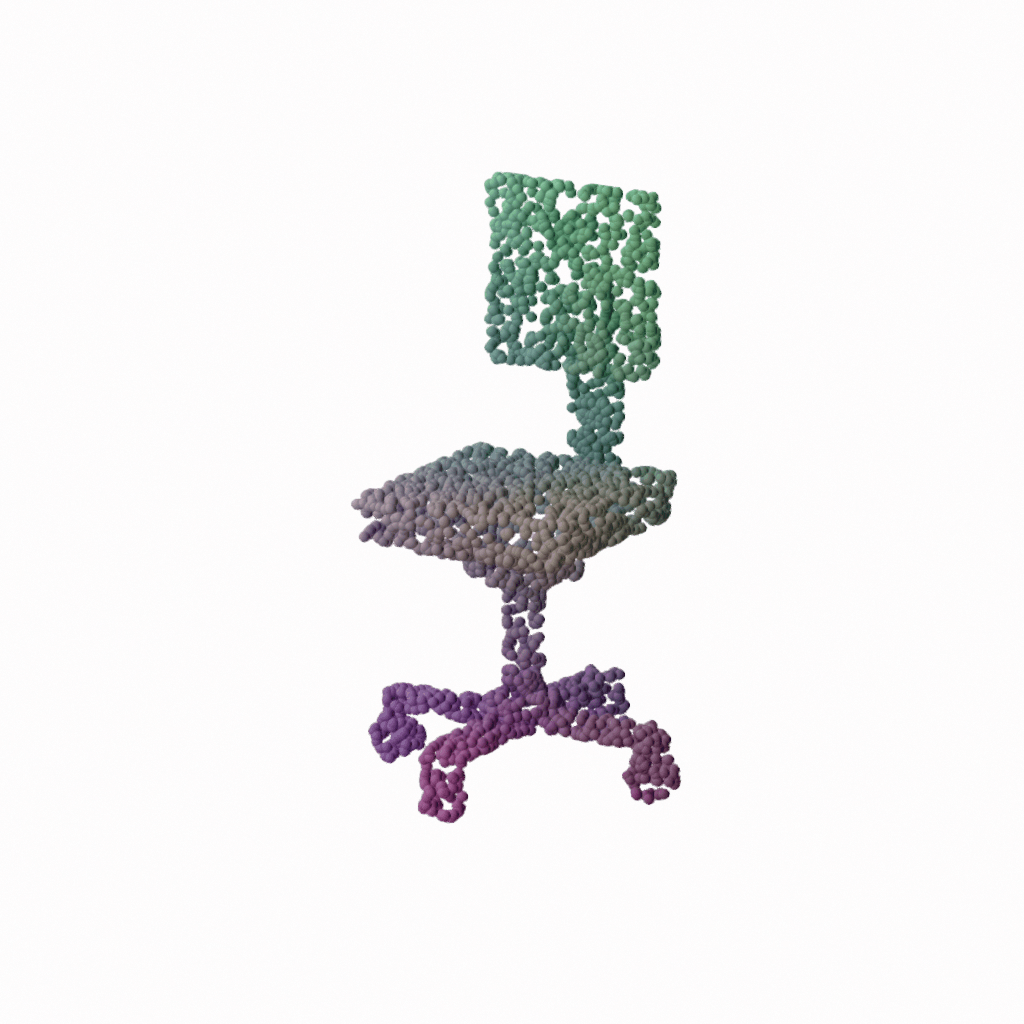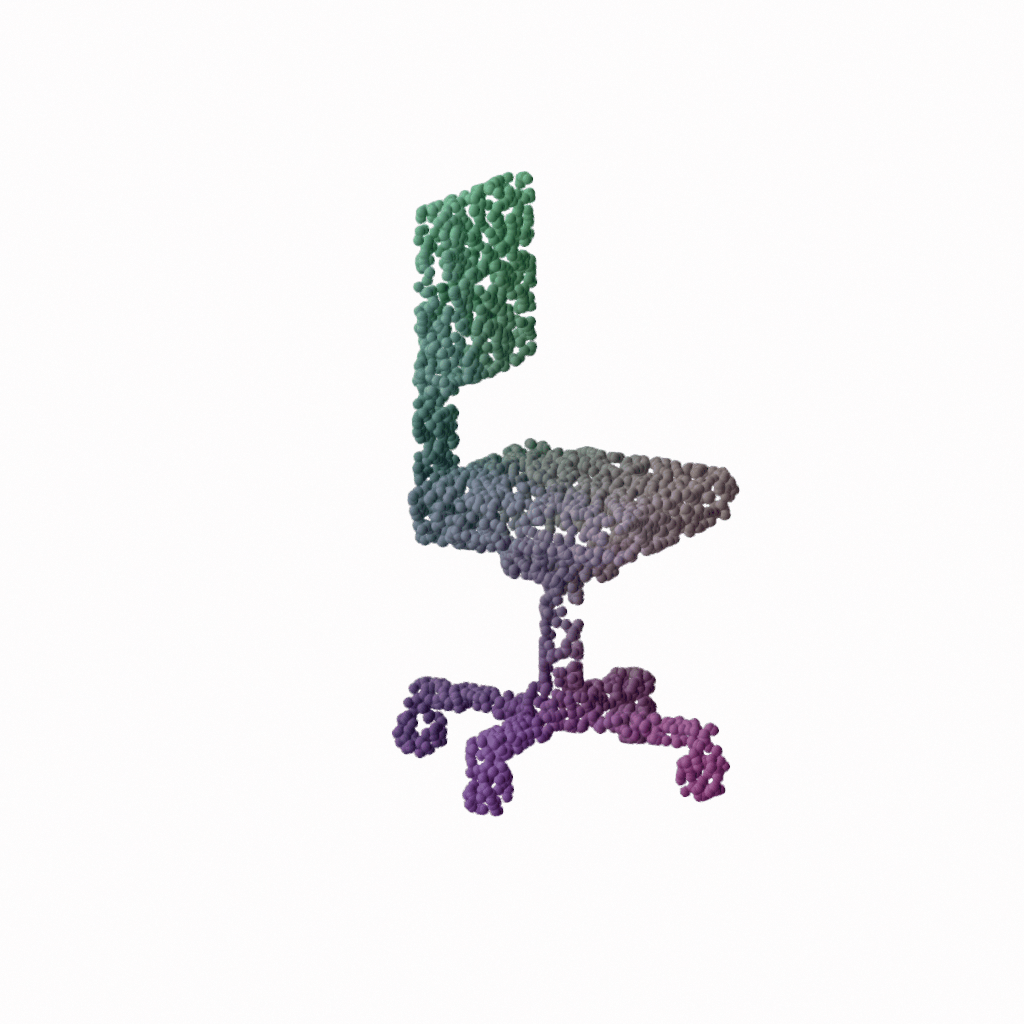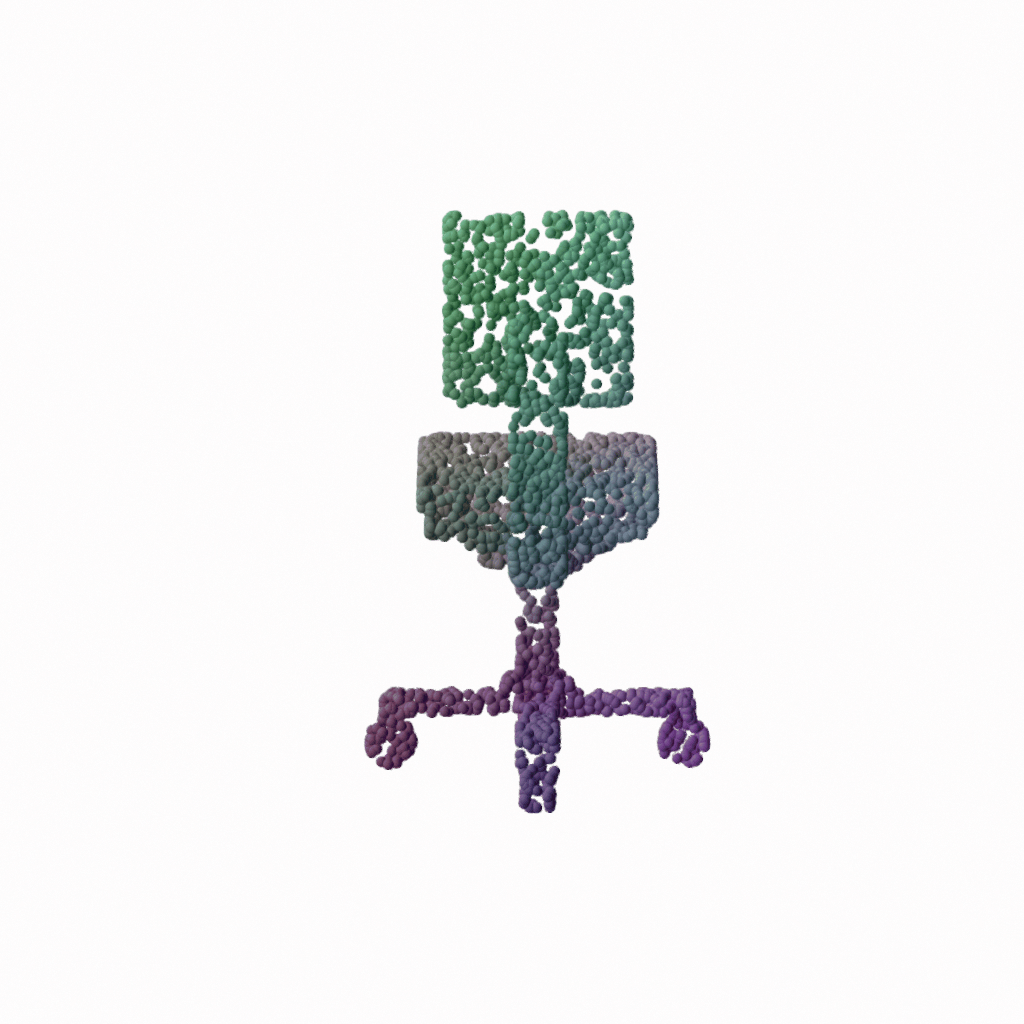
GeoUDF is a new learning-based framework reconstructing the underlying surface of a sparse point cloud. It consists of three modules, i.e., local geometry representation (LGR), geometry-guided UDF estimation (GUE), and edge-based marching cube (E-MC). Specifically, given a sparse 3D point cloud, we first model its local geometry through LGR, producing a dense point cloud associated with un-oriented normal vectors. Then we predict the unsigned distance field of the resulting dense point cloud via GUE, from which we customize and E-MC module to extract the triangle mesh for the zero level set. Each of the thress modules can be independently used as a general method in its own right.

The recent neural implicit representation-based methods have greatly advanced the state of the art for solving the long-standing and challenging problem of reconstructing a discrete surface from a sparse point cloud. These methods generally learn either a binary occupancy or signed/unsigned distance field (SDF/UDF) as surface representation. However, all the existing SDF/UDF-based methods use neural networks to implicitly regress the distance in a purely data-driven manner, thus limiting the accuracy and generalizability to some extent. In contrast, we propose the first geometry-guided method for UDF and its gradient estimation that explicitly formulates the unsigned distance of a query point as the learnable affine averaging of its distances to the tangent planes of neighbouring points. Besides, we model the local geometric structure of the input point clouds by explicitly learning a quadratic polynomial for each point. This not only facilitates upsampling the input sparse point cloud but also naturally induces unoriented normal, which further augments UDF estimation. Finally, to extract triangle meshes from the predicted UDF we propose a customized edge-based marching cube module. We conduct extensive experiments and ablation studies to demonstrate the significant advantages of our method over state-of-the-art methods in terms of reconstruction accuracy, efficiency, and generalizability.

Let be an sparse poitn cloud of points sampled from a surface , a quadratic polynomial surface is used to approximate the local surface:

and with such representation, we can densify through sampling 2D coordinates from a pre-defined local parameterization uniformly, obtaining , as well as its un-oriented normal vectors, .

Given a query point , we use the weighted distances to the tangent planes of its -NN neighbouring points, , to approximate its UDF,

where and . The gradient of UDF at could be approximate through weighted sum of ,

If the surface interacts with the connection between and , the following constraints must be satisfied,

Thus we could utilize the edge intersection detection on the connection between any two vertices of a cube, and find the most similar condition in the lookup table of Marching Cube to extract the triangles.

Here we show some visual results. The number of points is 3000 in the ShapeNet and MGN datasets, while for the ScanNet and ShapeNet Car datasets, the number of points is 6000. The model was only trained on the ShapeNet dataset. For more quantitative results, please refer to our paper.